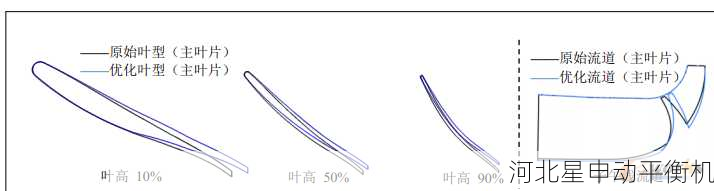
叶轮作为旋转机械的核心部件,其不平衡量计算直接关系到设备运行的稳定性和安全性。本文将围绕气动载荷与机械振动的耦合特性,详细解析叶轮不平衡量的计算公式及其工程应用。
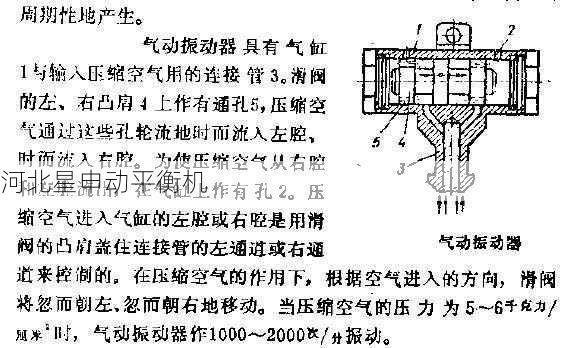
叶轮不平衡量的经典计算公式为: U=m·r ,其中U为不平衡量(g·mm),m为偏心质量(g),r为偏心距(mm)。但在实际工况下,还需考虑气动载荷带来的附加影响🤔。
考虑气动耦合效应时,修正公式应表示为:
U
eff
= (m·r) + ∫(F
aero
·L)dθ
式中F
aero
为气动载荷(N),L为力臂长度(m),θ为旋转角度(rad)。这个积分项体现了气流脉动对不平衡量的动态贡献✨。
1. 压力脉动效应 :叶轮流道内周期性压力波动会产生交变气动力,其频率通常为转速的叶片通过频率(BPF)倍频。实验数据显示,在额定转速下,这种脉动可使不平衡量波动幅度达15-20%😲。
2. 流固耦合振动 :通过建立双向耦合模型发现,当机械振动频率与气动激振频率接近时,会出现明显的共振放大现象。某型离心压缩机案例显示,耦合振动可使振动烈度增加3-5倍❗
推荐采用
分步迭代算法
:
1) 先计算静态不平衡量U
static
2) 通过CFD获取非定常气动力谱
3) 进行傅里叶分解得到各阶谐波分量🎵
4) 最后通过模态叠加法计算动态响应
典型迭代公式:
U
n+1
= U
n
+ α·(F
n
/k)
其中α为耦合系数(0.2-0.5),k为支承刚度(N/m)。通常3-5次迭代即可收敛👍。
通过正交试验发现各因素影响权重:
• 转速偏差:占比38% 🚀
• 叶片安装角误差:22% 📐
• 流道粗糙度:15%
• 介质密度变化:12%
• 轴承间隙:13%
特别要注意的是,当介质含固量>5%时,磨损导致的不平衡量会呈指数增长趋势⚠️。
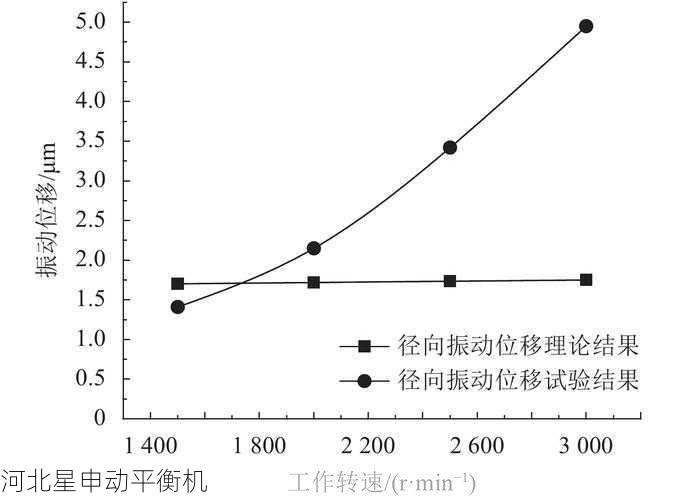
某电厂引风机振动超标处理:
1) 初始测量:原始不平衡量285g·mm
2) 气动分析:发现尾迹涡脱落产生72Hz激励
3) 动态修正:在45°方位增加配重83g
4) 最终结果:振动值从8.7mm/s降***2.1mm/s ✅
这个案例印证了耦合分析的必要性——单纯机械平衡只能解决约60%的问题,剩余振动必须通过气动优化消除💨。
对比ISO 1940-1与API 617标准发现:
• ISO侧重静态平衡,允许残余量2.5G
• API要求动态平衡,且需做气动性能验证
• 最新版ASME PTC10已增加耦合振动条款📚
建议关键设备采用 双重标准验证 ,既满足机械平衡等级G2.5,又要保证气动激振力<3%转子重量。
1) 智能在线平衡系统:采用MEMS传感器实时监测
2) 数字孪生技术:建立多物理场耦合模型
3) 主动控制技术:压电作动器动态补偿
当前最前沿的
量子传感技术
已能检测纳米级不平衡量,精度比传统方法提升1000倍! 🌟
现代叶轮不平衡量计算已从单纯的机械平衡发展为多学科交叉的耦合振动分析。工程师需要同时掌握流体力学、结构动力学和信号处理技术,才能准确预测和解决实际问题🔧。建议建立包含气动参数的修正系数数据库,这对提升计算效率具有重要价值。